平衡点（後編：グラフで考える）

前項に続き、次のような運動方程式があったとします。

　　\(m\dfrac{dv(t)}{dt}=mg-kv(t)^{2}\)　　\(v(0)=V_{0}\)、\(k>0\)

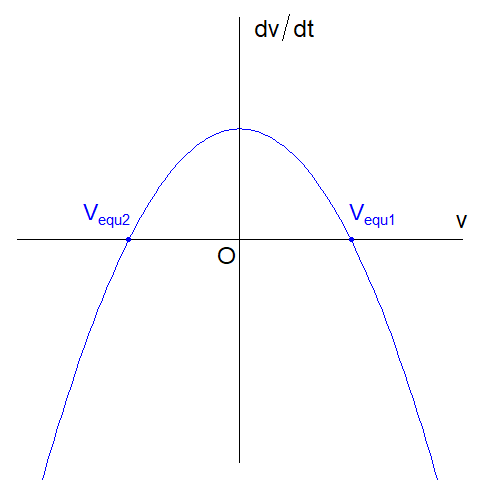
鉛直下向きに座標軸をとり、物体が初速度\(V_{0}\)で重力\(mg\)にひかれて空気抵抗\(-kv(t)^{2}\)を受けながら落ちてゆく運動を記述したものです。終端速度を考えてみます。 元の運動方程式で\(\dfrac{dv(t)}{dt}=0\)とおいて\(v(t)\)について解くと、 \(v(t)=\pm \sqrt{\dfrac{mg}{k}}\)になります。終端速度の候補が2つ出てきました。結論としては、 鉛直下向きに物体が落ちてゆくのだから、終端速度\(V_{ter}\)は\(+\sqrt{\dfrac{mg}{k}}\)になります。 これを示すためには、前項と同じように\(V_{equ, 1}=\sqrt{\dfrac{mg}{k}}\)、\(V_{equ, 2}=-\sqrt{\dfrac{mg}{k}}\)とおいて、\(v(t)=V_{equ,i}+\delta\) （\(\delta >0\)）が\(V_{equ,i}\)に近づくかどうかを調べれば良いはずです（\(i=1, 2\)）。 本稿では、それをグラフを使って調べてみます。 縦軸に\(\dfrac{dv(t)}{dt}\) 、横軸に \(v(t)\)を取って　 \(m\dfrac{dv(t)}{dt}=mg-kv(t)^{2}\)　 のグラフを書きます。すると、グラフの線が横軸と二つの点で交わることがわかります。これが\(V_{equ,1}\)、\(V_{equ,2}\)に相当します（下図）。

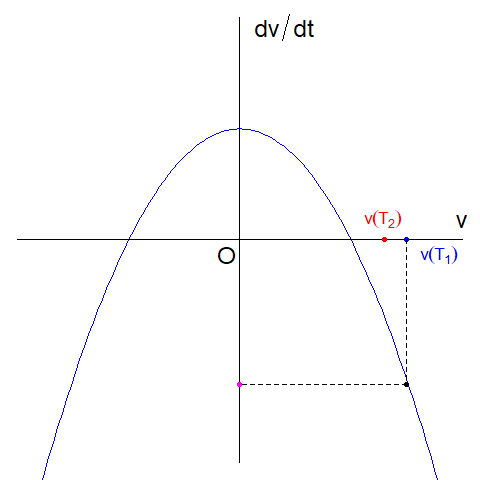
\(v(T_{1})=V_{equ,1}+\delta\)のとき（\(T_{1} \geq 0\)、\(\delta >0\)）、対応する\(\dfrac{dv(t)}{dt}\) は負の値（下図ピンク色の点）になることがわかります。つまり加速度が負の値なので減速します。時刻\(T_{2}(> T_{1})\)では加速した分だけ\(v(T_{2})\)は\(V_{equ, 1}\)に近づきます（下図）。

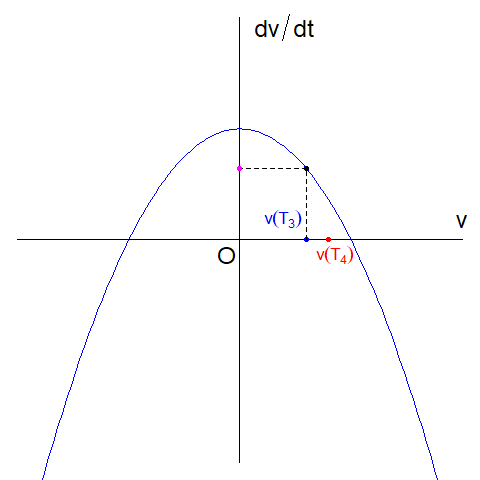
また、\(v(T_{3})=V_{equ,1}-\delta\)のとき（\(T_{3} \geq 0\)）、対応する\(\dfrac{dv(t)}{dt}\) は正の値（下図ピンク色の点）になることがわかります。つまり加速度が正の値なので加速します。時刻\(T_{4}(> T_{3})\)では加速した分だけ\(v(T_{4})\)は\(V_{equ, 1}\)に近づきます（下図）。

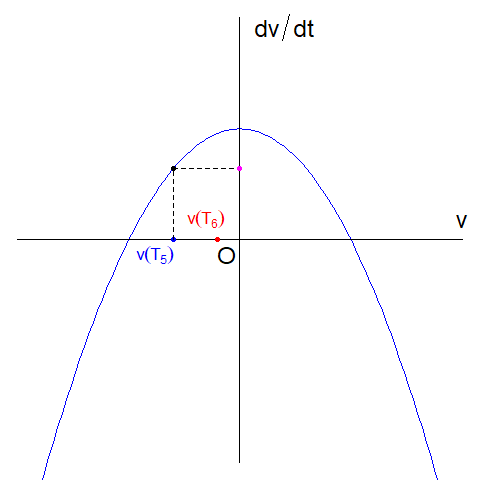
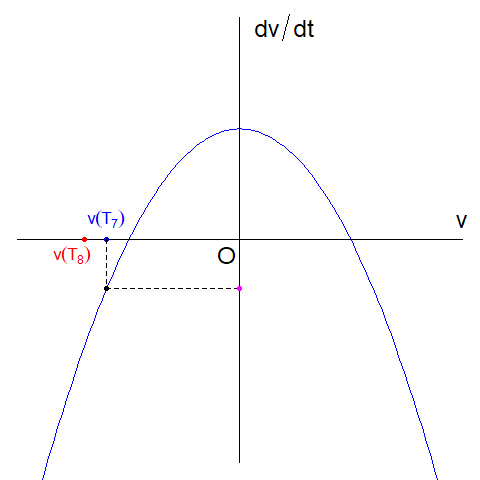
次に\(V_{equ, 2}\)を調べます。 \(v(T_{5})=V_{equ,2}+\delta\)のとき（\(T_{5} \geq 0\)）、対応する\(\dfrac{dv(t)}{dt}\) は正の値になることがわかります。つまり正の方向に加速します。時刻\(T_{6}(> T_{5})\)では加速した分だけ\(v(T_{6})\)は\(V_{equ, 2}\)から遠ざかります（左下図）。 また、\(v(T_{7})=V_{equ,2}-\delta\)のとき（\(T_{7} \geq 0\)）、対応する\(\dfrac{dv(t)}{dt}\) は負の値になることがわかります。つまり負の方向に加速します。時刻\(T_{8}(> T_{7})\)では加速した分だけ\(v(T_{8})\)は\(V_{equ, 2}\)から遠ざかります（右下図）。

以上をまとめます。 一般に、系が以下の微分方程式で記述されるとき

\(\dfrac{d \mathbf{x}}{dt}=\mathbf{f(x)}\)

\(\mathbf{f(x)}=0\)を満たす \(\mathbf{x}\) を平衡点と呼び、平衡点 \(\mathbf{x}\) の近傍にある全ての軌道が
\(\mathbf{x}\)に接近するとき、 \(\mathbf{x}\)は吸引的であるといい、 \(\mathbf{x}\)のことを沈点（吸引平衡点）という。
\(\mathbf{x}\)から離れるとき、 \(\mathbf{x}\)は反発的であるといい、 \(\mathbf{x}\)のことを源点（反発平衡点）という。

これらを見分けるためには、平衡点での傾きを調べればよさそうです。つまり平衡点での偏微分係数を求めてみて、それが

負の値ならその平衡点は吸引的、
正の値ならその平衡点は反発的

であることが分かります。実際にやってみます。

まずは偏導関数を求めます。

\(\dfrac{\partial}{\partial v} \left(\dfrac{dv}{dt}\right)= \dfrac{\partial}{\partial v} \left(mg-kv^{2}\right)=-2kv\)

次に\(v=V_{equ,1}\)、\(v=V_{equ,2}\)を代入したものが偏微分係数になります。

\(\dfrac{\partial}{\partial v} \left(\dfrac{dv}{dt}\right)|_{v=V_{equ ,1}}=-2kV_{equ,1}=-2k\sqrt{\dfrac{mg}{k}}<0\) （吸引的）

\(\dfrac{\partial}{\partial v} \left(\dfrac{dv}{dt}\right)|_{v=V_{equ ,2}}=-2kV_{equ,2}=2k\sqrt{\dfrac{mg}{k}}>0\) （反発的）

（注1） 実はこの運動方程式は解くことができます。 \(t=0\)のとき\(v=V_{0}\)、\(t=t\)のとき\(v=v(t)\)なので

\begin{align*} m\dfrac{dv}{dt} & =mg-kv^{2} \\ \dfrac{dv}{dt} & = -\dfrac{k}{m}\left(v-\sqrt{\dfrac{mg}{k}}\right) \left(v+\sqrt{\dfrac{mg}{k}}\right) \\ \end{align*} \(A=\sqrt{\dfrac{mg}{k}}\)とおいて \begin{align*} \dfrac{dv}{dt} & = -\dfrac{k}{m}\left(v-A\right) \left(v+A\right) \\ \dfrac{1}{\left(v-A\right) \left(v+A\right)}\dfrac{dv}{dt} & = -\dfrac{k}{m} \\ \dfrac{1}{2A} \left( \dfrac{1}{v-A} - \dfrac{1}{v+A} \right) \dfrac{dv}{dt} & = -\dfrac{k}{m} \\ \left( \dfrac{1}{v-A} - \dfrac{1}{v+A} \right) dv & = -2\dfrac{k}{m}A dt \\ \int_{V_{0}}^{v(t)} \left( \dfrac{1}{v-A} - \dfrac{1}{v+A} \right) dv & =\int_{0}^{t} \left( -2\dfrac{k}{m}A\right) dt \\ \left[ \ln \left(v-A\right) - \ln \left(v+A\right) \right]_{V_{0}}^{v(t)} & =\left[ -2\dfrac{k}{m}A\right]_{0}^{t} \\ \ln \left(\dfrac{v(t)-A}{v(t)+A}\right)-\ln \left(\dfrac{V_{0}-A}{V_{0}+A}\right) & =-2\dfrac{k}{m}At \\ \ln \left(\dfrac{v(t)-A}{v(t)+A}\right) &= \ln \left(\dfrac{V_{0}-A}{V_{0}+A}\right)+\ln \biggl(\exp \biggl(-2\dfrac{k}{m}At \biggr)\biggr) \\ \ln \left(\dfrac{v(t)-A}{v(t)+A}\right) &= \ln \left(\dfrac{V_{0}-A}{V_{0}+A} \exp \biggl(-2\dfrac{k}{m}At \biggr)\right) \\ \dfrac{v(t)-A}{v(t)+A} &= \dfrac{V_{0}-A}{V_{0}+A} \exp \biggl(-2\dfrac{k}{m}At \biggr) \\ \end{align*}
式を整理すると、

\(v(t) = \dfrac{1+\frac{V_{0}-A}{V_{0}+A} \exp(-2\frac{k}{m}At)}{1-\frac{V_{0}-A}{V_{0}+A} \exp (-2\frac{k}{m}At)}A\)

終端速度\(V_{ter}\)を求めたいのなら、\(t \to \infty\)とすればよいので

\(V_{ter}=A=\sqrt{\dfrac{mg}{k}}\)

となります。

（注2）本稿では、終端速度の候補として\(v(t)=- \sqrt{\dfrac{mg}{k}}\) が出てきましたが、速度の向きが鉛直下向きに設定されている落下運動であることから、 \(-\sqrt{\dfrac{mg}{k}}\) は終端速度になり得ません。物体が重力に逆らって鉛直上向きに飛んで行ってしまうことになります。では、なぜ\(v(t)=- \sqrt{\dfrac{mg}{k}}\) が出てきたのでしょうか。それは、元の運動方程式　\(m\dfrac{dv(t)}{dt}=mg-kv(t)^{2}\) が現実の全てを記述しているわけではないからです。この運動方程式は、鉛直下向きの落下運動をする物体の終端速度を求めるために簡素化されたモデル式であることに注意が必要です。今回のように方程式を調べて出てきた答えが、現実に起こる現象に対して妥当な結果であるかどうかは常に確認しなければなりません。

Tweet

前のページへ戻る

次のページへ進む

「我流の非線型物理学」へ戻る