蜘蛛の巣図

横軸に$X_0$、縦軸に$X_1$を置き、曲線$X_1=0.02(100-X_0)X_0$を描きます。$X_0=80$とすると、$X_1=32$です。

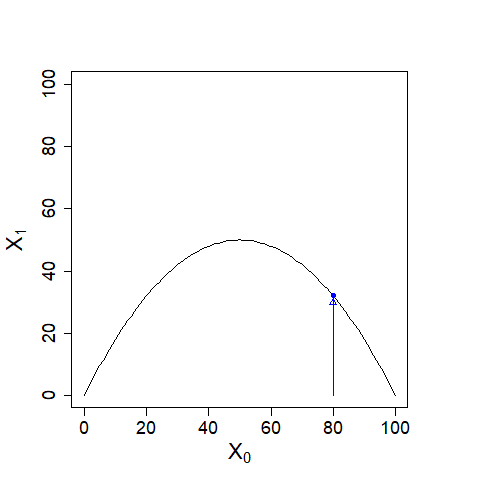
次に横軸に$X_1$、縦軸に$X_2$を置き、曲線$X_2=0.02(100-X_1)X_1$を描きます。$X_1=32$とすると、$X_1=43.52$です。

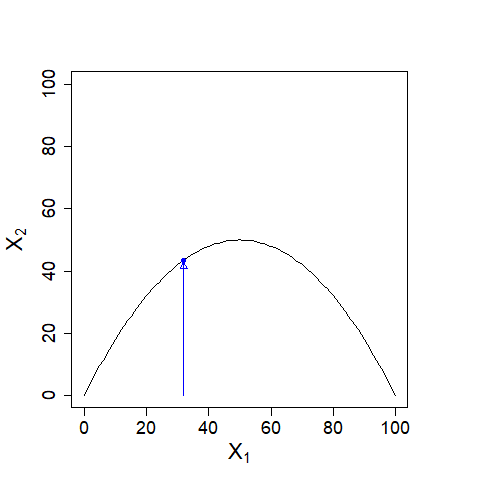
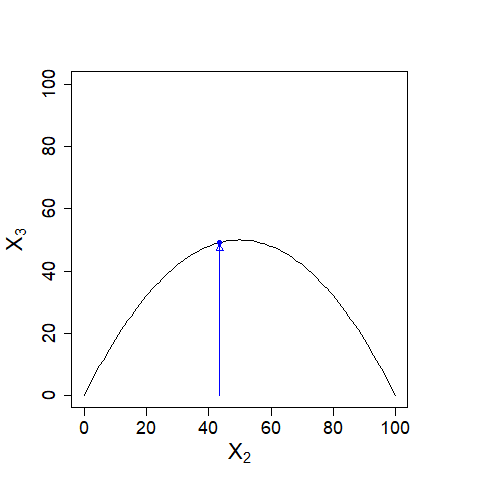
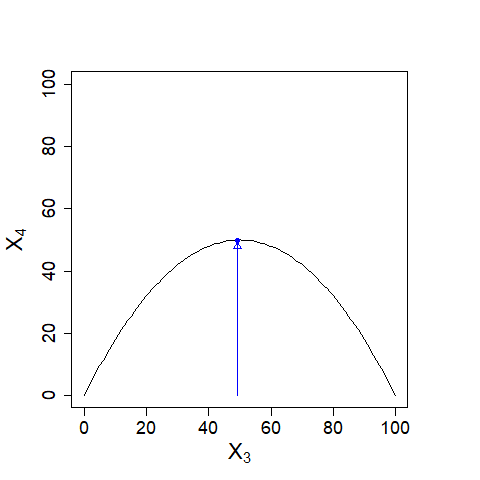
同じように$X_3$、$X_4$を求めて描いてゆくと$(X_n,X_{n+1})=(50,50)$に近づいていきます。

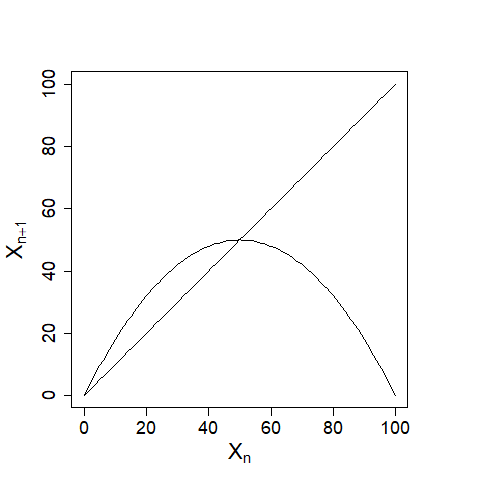
これらを一つの図にまとめられないでしょうか。縦軸に$X_{n+1}$、横軸に$X_n$を取り、曲線$X_{n+1}=0.02(100-X_n)X_n$と$X_{n+1}=X_n$を描きます（下図）。

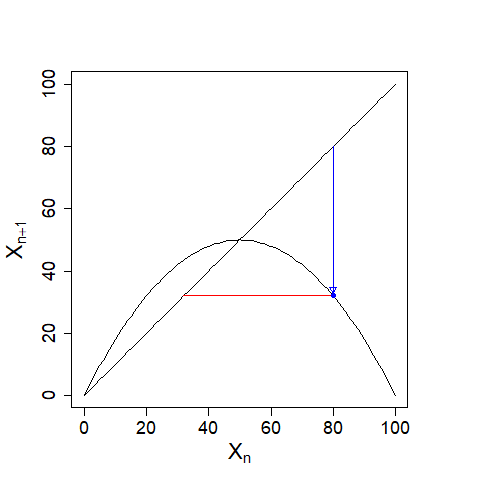
$(X_0,X_0)(=(80,80))$から$(X_0,X_1)$へ線（青線）を引きます。さらに $(X_0,X_1)$から$(X_1,X_1)$へ線（赤線）を引きます（下図）。

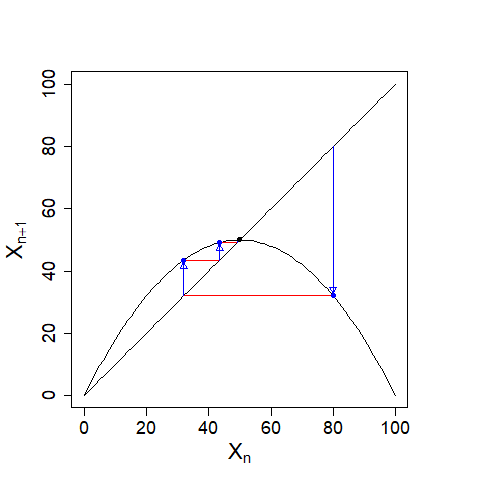
次に$(X_1,X_1)$から$(X_1,X_2)$へ線（青線）を引き、さらに $(X_1,X_2)$から$(X_2,X_2)$へ線（赤線）を引く、．．．ということを反復的に繰り返すことで$(X_n,X_{n+1})$が$(50,50)$に近づくことがわかります（下図）。

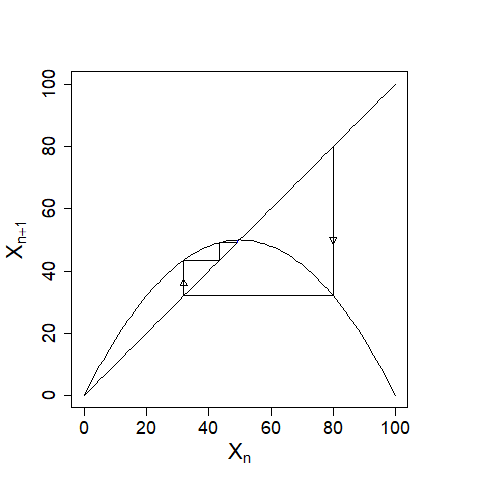
まとめると、縦軸に$X_{n+1}$、横軸に$X_n$を取り、適当な$X_0$を決めて（$k=0$として） (1) $(X_k,X_k)$から$(X_k,X_{k+1})$へ線を引く (2)$(X_k,X_{k+1})$から$(X_{k+1},X_{k+1})$へ線を引く (3)$k$を$1$大きくして(1)に戻る ということを反復的に繰り返すことで、$X_n$がどこへ向かうかが視覚的にわかります。以下のような図を『蜘蛛の巣図（web diagram）』といいます。矢印は向きがわかるように付ければ充分です。

Tweet

前のページへ戻る

次のページへ進む

「我流の非線型物理学」へ戻る